1 Defination of convolution
The mathmatical format of convolution is
- Continuous: $ Conv(x) = \int f(x-\alpha)t(\alpha)d\alpha $
- Discreate: $ Conv(x)=\sum_{\alpha} f(x-\alpha)t(\alpha) $
- Matrix: $ Conv(x) = (f * t)(x) $, where * represents the convolution process
2 Convolution Neural Network
2.1 Convolutional layer
Terms
- W: width or height of the input matrix (输入的长度或宽度)
- F: receptive field (感受野)
- S: stride(步幅)
- P: zero-padding (补零的数量)
- K: depth of the output (深度,输出单元的深度)
The output shape of after a convolution process follows: $$\frac{S}{W-F+2P} + 1$$
2.1.1 Convolutional Kernel
A convolutional kernel is a (x,x) matrix which walks through a depth slice with a predefined stride, and calculates the inner product within each step.
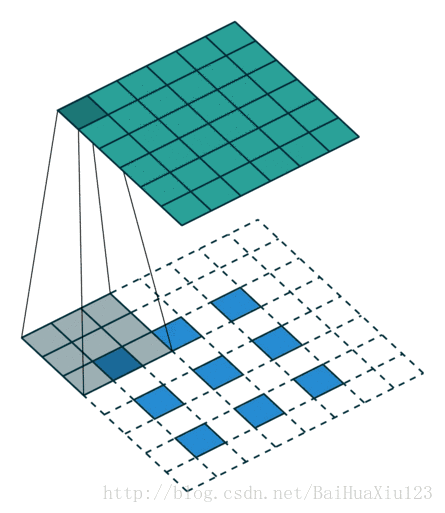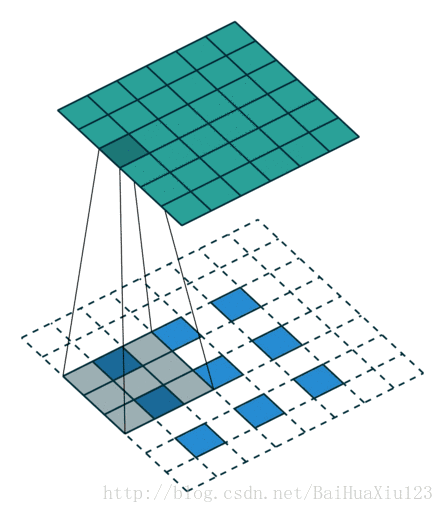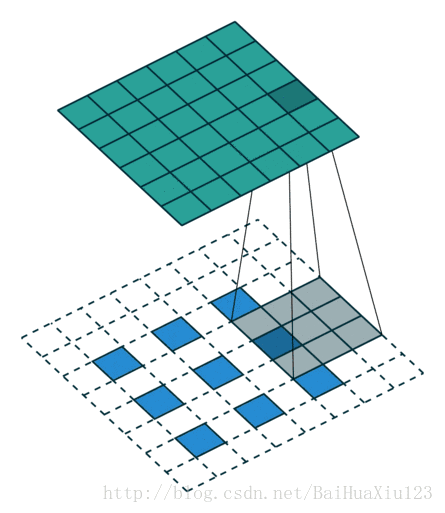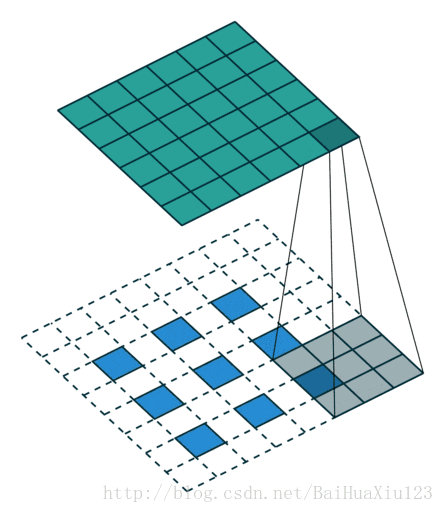
2.1.2 Parameter Sharing
We define layers at the same depth as depth slice. For example if the image mateix is (96,96,3), it contains 3 slices with each have 96x96 pixels. The depth slices are also known as channels.
Typically, neurons (units) in a slice share the same weight and convolutional kernel. This is for feature reduction since repeated units can identify features without considering their positions. This trick allows us control the size of the model and it guarantees better generalization ability.
2.1.3 ReLU Activation
ReLU abbreviates for rectified linear unit, which can be simply represented as max(0,x).
ReLU generates stable output since it is linear in the x > 0 space, there is no issue of gradient disapear.
Another advantage of ReLu is about sparse problem. We want every neurons play it’s role and maximize the ability of feature extraction, ReLU can amplify potential features with mean values while drop others.
2.2 Pooling Layer
Pooling, aka downsampling, is for feature reduction which reduce the size of the feature map generated by the convolutional layer. Pooling is independent from depth slices. There are several commonly used pooling methods:
- Max Pooling, which takes the maximum of the input matrix. This is the most common pooling method.
- Mean Pooling, which Takes the mean value of the input matrix.
- Gaussian Pooling. Borrowed from Gaussian Blur. Not commonly used.
- Trainable pooling. Trains a function that accepts a matrix as input while only output a single value. Not commonly used.
Full-connected Layer
This is a normal hidden layer where all elements inside the input vector connect all neurons within the layer. For CNN, the activation of the full-connected layers is softmax in most cases.
Model Stucture
